Кардио-ИТ

Качество в кардиологии
Медицинские Информационные Технологии
Рабочая группа

Метод оценки степени синхронизации низкочастотных колебаний в вариабельности ритма сердца и фотоплетизмограмме

Название журнала: 
Кардио-ИТ
Год: 
2016, №1
CID: 
e0101
Авторы: 
Киселев А.Р., Караваев А.С., Гриднев В.И., Прохоров М.Д., Пономаренко В.И., Боровкова Е.И., Шварц В.А., Посненкова О.М., Безручко Б.П.
Тип статьи: 
Оригинальная статья
Язык основного текста статьи: 
Русский
Тематика: 
Фундаментальные исследования в кардиологии
Резюме: 
В представленной статье подробно обсуждается предложенный авторами метод количественной оценки степени синхронизации низкочастотных колебаний (с основной частотой около 0,1 Гц) в вариабельности ритма сердца (ВРС) и фотоплетизмограмме (ФПГ), сопровождающийся контролем статистической значимости рассчитываемого значения индекса. Предложенный метод апробирован на примере 1056 пар записей ВРС и ФПГ обследуемых различного клинического статуса. Разработаны методические рекомендации по применению метода в клинических исследованиях.
Ключевые слова: 
низкочастотные колебания, вариабельность ритма сердца, фотоплетизмограмма, барорефлекс
Цитировать как: 
Киселев А.Р., Караваев А.С., Гриднев В.И., Прохоров М.Д., Пономаренко В.И., Боровкова Е.И., Шварц В.А., Посненкова О.М., Безручко Б.П. Метод оценки степени синхронизации низкочастотных колебаний в вариабельности ритма сердца и фотоплетизмограмме. Кардио-ИТ 2016; 3(1): e0101. [Kiselev AR, Karavaev AS, Gridnev VI, Prokhorov MD, Ponomarenko VI, Borovkova EI, Shvartz VA, Posnenkova OM, Bezruchko BP. Method of assessment of synchronization between low-frequency oscillations in heart rate variability and photoplethysmogram. Cardio-IT 2016; 3(1): e0101.]
DOI: 
10.15275/cardioit.2016.0101
PDF File: 
Иконка PDF cardio-it-2016-0101.pdf

 

Введение

Сложность организации сердечно-сосудистой системы (ССС) и механизмов ее регуляции обусловливает повышенный интерес исследователей к данной теме, при этом остается еще много нерешенных вопросов. Известно, что в ССС выявляется множество различных колебательных процессов различной природы, взаимодействующих между собой [1]. Для изучения механизмов регуляции ССС, в настоящее время, используются анализ вариабельности ритма сердца (ВРС) [2], вариабельности артериального давления [3], вариабельности периферического кровотока [4-7], взаимодействия различных колебаний в ССС между собой [7-13] и др. Некоторые авторы предлагали различные математические модели, описывающие контуры автономной регуляции кровообращения [14-17].

Среди всех периодических процессов, существующих в ССС, особое место занимают низкочастотные колебания с характерной частотой около 0,1 Гц (далее мы будем именовать их как «0,1 Гц-колебания»). Данные колебания выявляются на разных уровнях ССС, в частности, ВРС [2], вариабельности артериального давления [2], вариабельности фотоплетизмографического сигнала (примечание: в англоязычной литературе обычно именуется как «photoplethysmographic waveform variability (PPGV)», которую не следует путать с «pulse rate variability (PRV)») [9, 18].

0,1 Гц-колебания в ВРС и артериальном давлении обычно ассоциируют и с барорефлекторной, и с центральной нервной регуляцией [19-25]. Однако природа колебаний в этом частотном диапазоне в сигнале фотоплетизмограммы (ФПГ) вызывает дискуссии до сих пор. Наиболее распространенно мнение, что низкочастотные колебания в вариабельности ФПГ характеризуют симпатическую регуляцию периферического сосудистого тонуса [26-28]. Однако необходимо учитывать, что сигнал ФПГ содержит информацию как о периферическом кровотоке (включая микроциркуляторное русло), так и дистальном артериальном русле [29]. Это может объяснять наличие признаков центральной вегетативной регуляции в периферическом кровотоке, о чем сообщают некоторые авторы [30]. При этом систолические колебания кровенаполнения, анализируемые по данным ФПГ, похожи, но не идентичны таковым в вариабельности артериального давления на крупных артериях и в ВРС [31], хотя и могут отражать сходные механизмы сосудистой регуляции [32].

В наших ранее проведенных экспериментах с меняющимся по частоте дыханием от 0,05 Гц до 0,20 Гц была доказана функциональная независимость 0,1 Гц-колебаний, выявляемых в ВРС и ФПГ [9, 33]. При этом дополнительно было выявлено, что основная частота данных колебаний непостоянна и может варьировать в достаточно широких пределах [33], что обусловлено, вероятно, способностью регуляции ССС гибко адаптироваться к условиям функционирования.

Также нами ранее было выявлено, что 0,1 Гц-колебания в ВРС и ФПГ часть времени находятся в состоянии синхронизации порядка 1:1, т.е. взаимной подстройки мгновенных фаз и частот колебаний [18]. Это обеспечивает функциональное взаимодействие механизмов вегетативной регуляции разных отделов ССС. Однако для обеспечения адекватного взаимодействия их постоянная синхронизация не требуется. Например, у здоровых молодых лиц в состоянии покоя суммарная продолжительность участков синхронизации 0,1 Гц-колебаний колеблется в весьма широком диапазоне: от 20% до 60% от общего времени [18]. Для удобства оценки степени синхронизации 0,1 Гц-колебаний в ВРС и ФПГ была предложена количественная мера – суммарный процент фазовой синхронизации – индекс S. Данная мера показала свое потенциально важное клиническое значение, например, для оценки сердечно-сосудистого риска у пациентов, перенесших инфаркт миокарда [34, 35], контроля эффективности и безопасности медикаментозной терапии у пациентов с ишемической болезнью сердца и артериальной гипертонией [36-39], оценки вегетативной дисфункции у женщин в перименопаузе [40, 41], послеоперационного наблюдения за пациентами после аорто-коронарного шунтирования [42].

В данной статье приводится детальное описание методики диагностики синхронизованности 0,1 Гц-колебаний в ВРС и вариабельности ФПГ и расчета индекса   суммарного процента фазовой синхронизации S. Даются также методические рекомендации по использованию предложенного индекса S в клинической практике.

 

Материал и методы

Материал исследования

Клиническая применимость методики оценки синхронизации 0,1 Гц-колебаний в ВРС и ФПГ исследовалась в следующих группах испытуемых (всего 1056 записей):

  • 17 здоровых лиц (127 записей) (50% женщин), возраста 26±5 лет;
  • 41 пациент с перенесенным инфарктом миокарда около трех недель назад (34,4% женщин) (167 записей), возраста 55±9 лет;
  • 105 пациентов с артериальной гипертонией (762 записи) (62,9% женщин), возраста 46±7 лет.

Подобный клинически разнородный материал позволяет унифицировать рекомендации по использованию разработанной нами методики.

 

Регистрация биологических сигналов

Всем испытуемым синхронно регистрировалась электрокардиограмма (ЭКГ) во II стандартном отведении по Эйнтховену (рисунок 1а) и ФПГ с дистальной фаланги указательного пальца правой руки при помощи плетизмографического инфракрасного датчика отраженного света (рисунок 1б) в горизонтальном и, у некоторых пациентов, вертикальном положениях тела. Регистрация сигналов производилась многоканальным полирегистратором (электроэнцефалограф анализатор ЭЭГА-21/26 “Энцефалан-131-03”, модель 10 с комплектом стандартных датчиков, НПКФ "Медиком МТД”, Россия) с частотой дискретизации 250 Гц и разрешением 14 бит.

Продолжительность каждой записи составляла 10 минут. Во время регистрации сигналов дыхание у всех обследуемых было произвольным. Фрагменты типичных сигналов приведены на рисунке 1.

 


Рисунок 1. Типичный вид ЭКГ (а) и пульсограммы с сосудов микроциркуляторного русла (б) здорового человека. Оба сигнала приведены в произвольных единицах.

 

Первичная обработка данных

Для анализа ВРС из ЭКГ выделялась последовательность
R-R интервалов (Программа «Extracor». Свидетельство о государственной регистрации программы для ЭВМ №2010611339 от 16.02.2010 г.), т.е. кардиоинтервалограмма (КИГ) (рисунок 1а). Из-за изменчивости частоты сердечных сокращений точки в кардиоинтервалограмме расположены неэквидистантно по времени. Преобразование полученного неэквидистантного ряда в эквидистантный осуществлялась на основе его аппроксимации кубическими сплайнами и перевыборки значений через равные промежутки времени. Полученный эквидистантный ряд R-R интервалов с частотой дискретизации 4 Гц (в соответствии с Р.М. Баевским и соавторами [43]) использовался для дальнейшей обработки. Выделение 0,1 Гц-колебаний в ВРС и ФПГ (рисунок 2) производилось полосовой фильтрацией исходных сигналов (кардиоинтервалограммы и ФПГ) в диапазоне 0,06–0,14 Гц [43]. Отметим, что ширина полосы фильтрации выбрана нами после проведения специального исследования, применительно к различным клиническим задачам (на основе опыта предшествующих клинических исследований; см. раздел «Введение»).

 


Рисунок 2. Фурье-спектры мощности, построенные в линейном масштабе по сигналам кардиоинтервалограммы (а) и пульсограммы (спектр нормирования) с сосудов микроциркуляторного русла (б) здорового человека. Символом fv – отмечены пики в спектрах вблизи 0,1 Гц составляющих, символом fr – пики вблизи 0,3 Гц составляющих.

 

Определение мгновенных фаз сигналов

Системы биологической природы являются наиболее сложным объектом из всех известных. Для них характерно наличие большого числа взаимодействующих нелинейных элементов (т.е. для их математического описания необходимо использовать уравнения с нелинейными функциями). Их сигналы подвержены влиянию шумов различной природы и, как правило, нестационарны (параметры систем породивших сигналы и статистические свойства сигналов изменяются во времени). Поэтому для изучения индивидуального поведения элементов живых систем и особенностей их взаимодействия приходится развивать и использовать специализированные методы [44, 45].

Развитием методов обработки и анализа сигналов сложных, в том числе, живых систем исторически занимается радиофизика и ее подраздел – нелинейная динамика – область знаний, ориентированная на исследование колебаний и волновых процессов. При этом предполагается, что теории, подходы и методы, развиваемые в рамках нелинейной динамики, универсальны. То есть результаты, полученные для колебательных систем одной природы (как правило, хорошо изученных электронных радиофизических систем и их математических моделей), могут быть использованы для изучения систем другой природы, например, биологических объектов. Подобная универсальность подходов и методов обсуждается в рамках концепции синергетики [46, 47]. Одним из важных, но наиболее непривычных вопросов при анализе сложных сигналов, является анализ мгновенных фаз колебаний исследуемых систем. В данном разделе обсуждается вопрос определения понятия и изучения свойств мгновенных фаз, и приводятся некоторые примеры.

Некоторые основные понятия, с которыми оперирует радиофизика и нелинейная динамика, иллюстрируются на рисунке 3. В примере, представленном на рисунке 3, в качестве изучаемого сигнала системы выступает зависимость от времени координаты отклонения маятника от положения равновесия – x(t) (рисунок 3а). В нелинейной динамике эту величину называют еще «динамической переменной», а ее представление в дискретном виде, пригодном для анализа и обработки на компьютере – «временным рядом», «реализацией» или «временной реализацией» [44, 45].

 

  
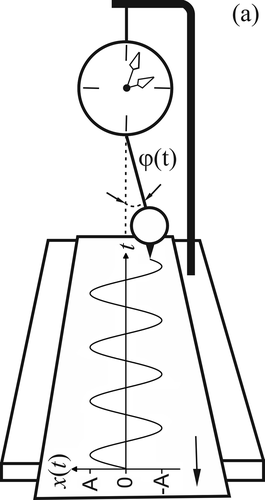
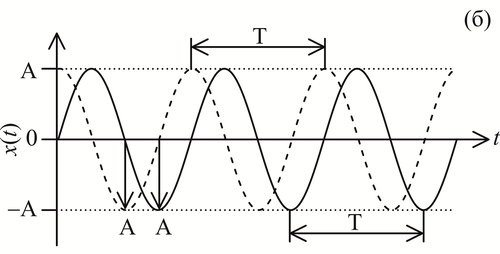
Рисунок 3. Иллюстрация некоторых основных понятий радиофизики на примере колебаний маятниковых часов: (а) – регистрация колебаний маятника с помощью закрепленного на нем маркера, чертящего на бумажной ленте, которая протаскивается с фиксированной скоростью под маятником; (б) – примеры сигналов зависимостей координаты маятника x от времени t, зарегистрированных с маятниковых часов. Сплошная линия – маятник запущен с нулевой начальной фазой ϕ(t)=0, пунктир – с ненулевой начальной фазой ϕ(t)= ϕ0 (см. панель (в)); (в) – иллюстрация различных фаз колебаний маятника. В данном примере фаза имеет смысл угла между подвесом маятника и условной вертикальной линией   его положением равновесия.

 

Показано, что зависимость от времени координаты маятника часов могут быть с высокой точностью описаны гармонической функцией, т.е. тригонометрической функцией синус или косинус (формула 1) [48].

x(t) = A sin(2πft + φ0)                     (1)

Графическое изображение сигнала x(t) представлено на рисунке 3б. В выражении (1) есть несколько параметров: A – амплитуда колебаний, т.е. максимальное отклонение подвеса от положения равновесия, которое можно измерить, например, в сантиметрах; f=1/T – частота (линейная частота) колебаний (измеряется в герцах – Гц), т.е. количество полных колебаний, совершаемых маятником за 1 секунду; период T (рисунок 3б) – величина обратная частоте – время, через которое форма сигнала будет полностью повторяться. Для удобства записи при расчетах часто используется т.н. круговая частота, однозначно связанная с линейной частотой выражением: ω=2πft. Выражение под аргументом функции sin в формуле (1) называется «мгновенной фазой» и имеет смысл количества периодов колебаний, пройденных системой к моменту времени t после начала измерений (формула 2).

φ(t) = 2πft + φ0 = ωt + φ0                     (2)

Как следует из определения и видно из формулы (2), мгновенная фаза – это величина, которая никогда не убывает, а может только нарастать во времени, в общем случае, с изменяющейся скоростью. Мгновенная фаза измеряется в радианах или градусах (которые однозначно связаны). За период колебаний мгновенная фаза нарастает на 2π радиан или на 360 градусов, что то же самое. φ0 – начальная фаза колебаний, в нашем примере имеет смысл угла, на который был отведен маятник в начале измерений (рисунок 3в).

На рисунке 3б сравниваются сигналы x(t) c разной начальной фазой: сплошная линия φ0=0, пунктир – φ0≠0. Говорят, что сигналы, представленные на рисунке 3б, сдвинуты по фазе или повернуты по фазе относительно друг друга.

Как видно из формулы (2), мгновенная фаза гармонического сигнала (считающегося эталонным, самым простым сигналом в радиофизике) нарастает с постоянной скоростью строго линейно (т.е. график ее зависимости от времени является прямой линией). По определению, скорость изменения во времени некоторой величины является производной по времени ее координаты. Продифференцировав φ(t) из выражения (2) получим формулу (3).

φ(t) = ω                                 (3)

Производная по времени мгновенной фазы называется «мгновенной частотой» (для периодических колебаний это постоянная величина, не зависящая от времени: ω=2πft. Так как геометрический смысл производной – угол наклона графика в данной точки относительно горизонтальной оси, то видно, что угол наклона φ(t) тем выше, чем выше мгновенная частота колебаний в данный момент времени. Для периодических колебаний с неизменной частотой мгновенная фаза будет нарастать с неизменным углом, пропорциональным частоте колебаний (формула 3).

При анализе колебаний простой формы введение понятия мгновенной фазы может показаться излишним, однако, оказывается, что при исследовании сложных сигналов она является очень информативной и чувствительной величиной, позволяющей описать свойства колебаний сложной формы [49]. Однако, при анализе непериодических колебаний, есть трудности с введением самого понятия мгновенной фазы, т.к. не могут быть строго введены базовые понятия периода и частоты. В этом случае обычно оперируют понятиями: «мгновенный период» и «мгновенная частота» и их усредненными значениями: «характерный период» и «характерная частота». Как правило, в этом случае строго выразить мгновенную фазу точной формулой (аналогично выражению (2)) не удается и приходится использовать приближенные формулы и численные методы. Например, при анализе сигнала ЭКГ длительность одного RR-интервала естественным образом определяет мгновенный период процесса сердцебиения, а усредненная величина – частота сердечных сокращений (ЧСС) – характерный период.

При анализе сигналов с хорошо выраженным периодом и сигналов импульсной формы, часто используется определение мгновенной фазы через сечение. На рисунке 4 иллюстрирует-ся введение мгновенной фазы сигнала ЭКГ этим способом. Мгновенным периодом полагается интервал между пересечениями нарастающим фронтом зубца R выбранного сечения x(t)=s (рисунок 4а). При этом полагается, что между двумя такими последовательными пересечениями мгновенная фаза сигнала линейно нарастает на 2π. Из рисунка 4б видно, что фаза непериодического сигнала нарастает нелинейно, неся информацию о характере сигнала. При реализации некоторых методов, основанных на анализе фазовой динамики, оказывается удобным использование так называемой «свернутой мгновенной фазы» (рисунок 4в), однозначно выражаемой из развернутой мгновенной фазы (рисунок 4б) путем вычисления остатка от деления последней на 2π (обычно записывают:  φ(t) mod 2π). Сигнал развернутой мгновенной фазы также всегда может быть вычислен из свернутой. Сигнал мгновенной фазы, в случае анализа ЭКГ, может использоваться, например, для диагностики и количественного анализа аритмий [50] и решения других фундаментальных и прикладных задач [51-53].

 


Рисунок 4. Введение мгновенной фазы для сигнала ЭКГ: (а) – сигнал ЭКГ с сечением и отмеченными границами мгновенных периодов; (б) – введенная методом сечений мгновенная фаза сигнала ЭКГ; (в) – свернутая фаза.

 

Анализ мгновенной фазы ЭКГ может оказаться удобным при анализе расстояния между зубцами PQRST-комплекса. В этом случае, их положение, выраженное в единицах мгновенной фазы, оказывается привязанным не просто к абсолютному времени, а к фазе сердечного цикла.

Из рисунка 4а видно, что введение фазы сигнала указанным способом имеет некоторый произвол, в частности, положение сечения s может быть выбрано по-разному, что несколько влияет на результат. Однако наличие такого произвола при анализе сложных непериодических сигналов является неизбежной платой за использование методов анализа фазовой динамики. Универсального решения этой проблемы не существует.

На рисунке 5 приведены еще несколько примеров введения мгновенной фазы с помощью сечения линией x(t)=0  для разных сигналов. Видно, что фаза сигнала, амплитуда которого заметно меняется, может расти линейно (рисунок 5б), аналогично гармоническому сигналу на рисунке 5а. Вместе с тем, фаза сигнала с постоянной амплитудой и изменяющейся частотой отражает изменения последней (рисунок 5в). При этом выделение из сигнала, приведенного на рисунке 5в, сигнала мгновенной фазы фактически является единственным способом количественно охарактеризовать свойства такого сигнала. Приведенные на рисунке 5(а-в) примеры иллюстрируют целесообразность и возможность раздельного анализа амплитуд и фаз сигналов сложной формы.

При анализе сложных сигналов наглядный метод с введением секущей дает погрешности, связанные с предположением о линейном характере роста мгновенной фазы на характерном периоде. Поэтому чаще используются другие подходы, связанные с восстановлением проекции фазового портрета [49, 52, 54-56]. Наиболее часто используется метод, основанный на использовании преобразования Гильберта, представляющего собой идеальный широкополосный фазовращатель на –π/2 [57, 58]. Т.е. все гармоники Фурье-разложения преобразованного по Гильберту сигнала сдвигаются по фазе на –π/2. Например, если сигнал представлял собой функцию косинуса, то его преобразование Гильберта представляет собой синус с такой же частотой и амплитудой.

Для введения фазы строится плоскость, на которой по осям откладывают сам сигнал x(t) и его преобразование Гильберта – h(t). Например, для гармонических сигналов изображающая точка (точка с координатами (x(t), h(t))) будет двигаться во времени вокруг центра координат по окружности. Для сигналов сложной формы траектория движения изображающей точки более сложная. Мгновенная фаза сигнала φ(t) определяется, как угол между осью координат и линией, соединяющей центр координат построенной плоскости (точку с координатами (0, 0)) и изображающую точку (рисунок 5г) [49].

Для гармонических сигналов результат введения мгновенной фазы с помощью любого метода (метода секущей, преобразования Гильберта и других) совпадает друг с другом и с определением (2). Однако для сигналов сложной формы разные методы введения мгновенной фазы дают несколько отличающиеся результаты. В общем случае, считается, что преобразование Гильберта позволяет выделить мгновенную фазу сигнала точнее, чем метод, основанный на использовании сечения [49, 59].

 

    
Рисунок 5. Примеры мгновенных фаз колебаний для разных сигналов: (а) – гармонический сигнал, фаза растет строго линейно с постоянной скоростью; (б) – сигнал сложной формы с изменением амплитуд сигналов, однако фаза также растет линейно; (в) – амплитуда сигнала постоянна, однако, мгновенная изменяется, реагируя на изменение во времени частоты; (г) – пример введения мгновенной фазы гармонического сигнала с помощью преобразования Гильберта.

 

Анализ фазовой динамики взаимодействующих систем

Особенное значение анализ фазовой динамики имеет при исследовании взаимодействующих систем. Оказывается, что мгновенные фазы колебательных систем наиболее чувствительны к появлению между системами слабой связи [44, 45, 60-62]. В этом случае, с ростом связи, сначала изменения в динамике систем проявляются в их фазах, а лишь затем могут быть диагностированы по амплитудам. Разработан и успешно применяется для анализа систем биологической природы целый ряд методов диагностики связанности, основанных на анализе фазовой динамики [63-65].

Особый интерес представляет изучение явления фазовой синхронизации между системами, когда при появлении достаточно сильной связи фазы взаимодействующих коле-бательных систем подстраиваются друг под друга, причем амплитуды при этом могут изменяться хаотически и не коррелировать [66-70]. Пример такого поведения сигналов взаимодействующих систем представлен на рисунке 6. Участок 1 соответствует несинхронному поведению сигналов x(t) и y(t) (рисунок 6а). Момент времени, отмеченным первым вертикальным пунктиром, соответствует увеличению силы связи между системами, что привело к возникновению фазовой синхронизации систем – участок 2 на рисунке 6. В момент, отмеченный вторым вертикальным пунктиром, связь уменьшилась, что привело к десинхронизации систем (участок 3 графиков).

Рассчитанные с помощью преобразования Гильберта мгновенные фазы сигналов x(t) и y(t): φx(t) и φy(t), соответственно, представлены на рисунке 6б. На интервалах несинхронного поведения 1 и 3 фазы растут независимо друг от друга. Интервал 2 соответствует синхронному поведению. Видно, что в каждый момент времени углы наклона мгновенных фаз на этом участке равны друг другу (рисунок 6б), т.е. совпадают мгновенные частоты колебаний.

 


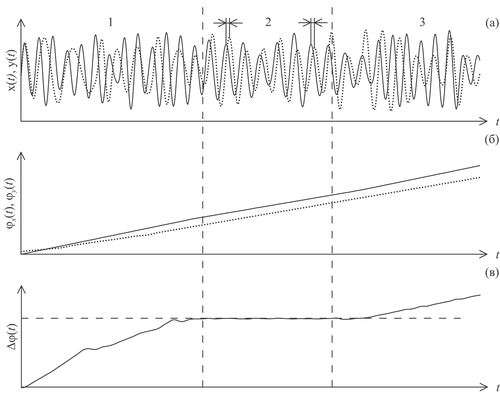
Рисунок 6. Синхронизация колебательных систем: (а) – сигналы взаимодействующих систем; (б) – мгновенные фазы сигналов x(t) и y(t) введенные с помощью преобразования Гильберта; (в) – разность мгновенных фаз. Вертикальные пунктирные линии отмечают моменты изменения силы связи между системами: левая линия – увеличение связи, приведшее к фазовой синхронизации (участок 2 графиков), правая линия – уменьшение связи, вызвавшее десинхронизацию (участок 3 графиков).

 

Удобным способом наблюдения фазовой синхронизации является вычисление разности мгновенных фаз – Δφ(t). По определению фазовой синхронизации [49], синхронным интервалам соответствует ситуация:

Δφ(t) = |φx(t) - φy(t)| < C,                      (4)

где C – небольшая константа. Т.е. участкам фазовой синхронизации соответствуют горизонтальное плато на разности фаз Δφ(t), где Δφ(t) может немного колебаться относительно условной горизонтальной линии под влиянием шумов, неизбежно присутствующих в любых экспериментальных сигналах. Такой участок (интервал 2 между вертикальными пунктирами) хорошо виден на рисунке 6в. Участки несинхронного поведения соответствуют нарастанию кривой на графике Δφ(t) (участки 1 и 3).

Таким образом, участки фазовой синхронизации детектируются, как интервалы экспериментальных реализаций, на которых разность фаз между экспериментальными сигналами остается постоянной в течение нескольких характерных периодов колебаний. Часто синхронные участки можно выявить визуально, совместив на одном графике исследуемые сигналы (см. участок 2 на рисунке 6а). Однако, наиболее надежная диагностика и количественный анализ возможны только с помощью расчета разности мгновенных фаз.

 

Анализ фазовой синхронизации 0,1 Гц-колебаний в ВРС и ФПГ

Анализ фазовой динамики и фазовой синхронизации широко распространен в том числе, при анализе записей биопотенциалов человека [71-73]. Для этого был разработан целый ряд методов, включая функцию когерентности [74], синхрограммы [75, 76], коэффициент фазовой когерентности [49], методы, основанные на вейвлет-преобразовании [77-80] и др. Однако при анализе данных сложных биологических объектов, как правило, приходится модифицировать существующие подходы или разрабатывать новые, ориентируясь на специфику сигналов конкретных изучаемых систем. Нами был предложен метод, позволяющий диагностировать фазовую синхронизацию контура барорефлекторной регуляции тонуса артериальных сосудов и контура регуляции частоты сердечных сокращений [9, 33, 61, 81]. Как показали проведенные исследования [82], при анализе сигналов контуров регуляции ССС предложенный метод отличается более высокой чувствительностью, благодаря тому, что он специально ориентирован на анализ нестационарных данных, для которых характерно спорадическое чередование синхронных и несинхронных участков, аналогично представленному на рисунке 6 примеру.

Предложенный метод диагностики фазовой синхронизации включает следующие этапы обработки и анализа данных:

  • одновременная регистрация сигналов ЭКГ и ФПГ;
  • выделение из сигнала ЭКГ последовательности длительностей R-R интервалов (т.е. КИГ);
  • расчет эквидистантной КИГ с частотой дискретизации 5 Гц с помощью аппроксимации [2, 43];
  • фильтрация сигналов эквидистантной КИГ и ФПГ в полосе [0,05; 0,15] Гц для выделения сигналов исследуемых контуров регуляции;
  • прореживание фильтрованного сигнала ФПГ до частоты дискретизации 5 Гц;
  • выделение с помощью преобразования Гильберта мгновенных фаз колебаний;
  • расчет разности мгновенных фаз Δφ(t).

Регистрация данных может осуществляться любым цифровым устройством, обеспечивающим одновременную запись одного отведения ЭКГ и одного канала пальцевой ФПГ отраженного или проходящего света. Регистратор должен обеспечивать передачу зарегистрированных данных в компьютер для анализа и обработки. Полоса пропускания регистратора должна быть не уже 0,05-60 Гц для обоих каналов, частота дискретизации не менее 120 Гц, разрядность квантования не менее 14 бит [83]. Учитывая, что характерный период исследуемых ритмов составляет порядка 10 секунд, требования к аппаратной части потенциально могут быть снижены, однако, это требует проведения специального исследования.

Как было ранее показано в наших работах, возможна диагностика синхронизованности по единственному сигналу ФПГ, из которого с помощью разработанной нами методики выделяется информация о сердечном ритме [84, 85].

Интервалы синхронизации диагностировались с помощью разработанной автоматической процедуры. В силу наличия в экспериментальных данных исследуемых систем шумов различной природы, диагностика пологих участков разности мгновенных фаз является нетривиальной задачей. Для снижения влияния флуктуаций, связанных с действием шумов, была предложена методика, основанная на линейной аппроксимации Δφ(t) в скользящем окне. Для этого с помощью метода наименьших квадратов [86] в скользящем окне шириной b (секунд) к временному ряду Δφ(t) подгонялось уравнение прямой. Суть этой процедуры заключается в том, что исходно неизвестные коэффициенты α и β абстрактного уравнения линии: z(t) = αt + β подбираются по участку сигнала длиной b таким образом, чтобы линия “прошла между” экспериментальными точками зашумленного экспериментального временного ряда Δφ(t) (тонкая линия на рисунке 7). Коэффициент α = tgγ отвечает за угол наклона γ линии z(t) относительно горизонтальной оси (отмеченной горизонтальным пунктиром на риcунке 7). α имеет смысл производной мгновенной разности фаз, т.е. мгновенной расстройки частот в данный момент времени (3). Если линия z горизонтальна, что должно наблюдаться на синхронных участках, то α = γ = 0. При анализе экспериментальных данных в силу неизбежного наличия шумов и ошибок, связанных с конечной точностью вычислений, аппроксимирующая линия z будет почти всегда немного отклоняться от горизонтали, что учтено при реализации предложенного метода диагностики синхронизованности.

 


Рисунок 7. Иллюстрация работы метода автоматического поиска участков фазовой синхронизации по сигналу разности мгновенных фаз Δϕ(t). Границы интервала фазовой синхронизации отмечены вертикальными пунктирными линиями.

 

В силу нестационарности и сложной формы сигналов исследуемых систем возможны кратковременные случайные совпадения мгновенных частот колебаний даже несвязанных систем, проявляющиеся появлением коротких пологих участков разности фаз. Для исключения из анализа таких ситуаций вводится ограничение на минимальную длительность выявленных синхронных участков l (секунд) (около 2 характерных периодов колебаний).

Нами было проведено специальное исследование, направленное на выбор значений свободных параметров предложенного метода диагностики фазовой синхронизации контура симпатической регуляции ЧСС и контура регуляции тонуса артериальных сосудов у людей, для повышения чувствительности и специфичности метода. Полученные значения параметров составили: b=13 (c), |α|≤0,01, l=16 (c) [81].

Таким образом, предложен алгоритм поиска участков фазовой синхронизации с помощью предложенного подхода по временной реализации разности мгновенных фаз сигналов исследуемых систем:

  • Берется участок (при анализе данных обычно используют термин «скользящее окно») длительностью b секунд, по которому методом наименьших квадратов подгоняется уравнение линии z и вычисляется угловой коэффициент этой линии – α.
  • Берется следующий интервал той же длины (скользящее окно) Δφ(t), сдвинутый на один дискретный отсчет (минимально возможный шаг по времени) относительно предыдущего и рассчитывается следующее значение α. Процедура повторяется многократно, т.е. скользящее окно, в котором каждый раз рассчитывается новое значение α проходит по всему сигналу Δφ(t).
  • Если на интервале длиной не менее l секунд в нескольких последовательных скользящих окнах аппроксимирующая прямая z остается близкой к горизонтали (модуль углового коэффициента наклона |α| не превышает выбранного значения 0,01), то такой интервал считается интервалом фазовой синхронизации исследуемых систем.

В качестве количественной меры, характеризующей степень синхронизации систем, был предложен суммарный процент фазовой синхронизации – индекс S [9, 18]. Для его расчета длительности всех выявленных участков синхронизации суммируются, делятся на продолжительность записи сигналов, и результат выражается в процентах.

 

Анализ статистической значимости суммарного процента фазовой синхронизации

Для сложных нестационарных сигналов живых систем характерны случайные флуктуации частоты и фазы. При этом возможны случайные совпадения фаз и частот колебаний (даже для несвязанных сигналов), которые могут быть ложно детектированы, как интервалы фазовой синхронизации. Такие события будут искажать значение рассчитываемого индекса S, снижая специфичность результатов [87]. Появление ложных выводов о наличии синхронизации особенно вероятны в случае, если характерные частоты анализируемых сигналов близки друг к другу.

Поэтому при анализе экспериментальных данных может оказаться важным оценивать вероятность того, что рассчитанное значение S получено не в силу случайных флуктуаций сигналов, а за счет особенностей динамики взаимодействия породивших сигналы систем. Такая процедура называется оценкой статистической значимости результатов. В большинстве наших работ статистическая значимость оценивалась c использованием подхода, основанного на генерации ансамбля искусственно приготовляемых суррогатных данных [88, 89]. Это данных, сохраняющие некоторые статистические свойства исходных сигналов, однако связи, которые могли существовать между ними, заведомо разрушаются.

Наиболее широко нами использовались так называемые «AAFT» (Amplitude Adjusted Fourier Transform) суррогатные данные, с помощью которых проверяется статистическая гипотеза о несвязанных линейных системах [90, 91].

Метод основан на том, что у периодограмм зарегистрированных сигналов (Фурье-спектры мощности, оцененные без усреднения по временным реализациям сигналов), задается случайное распределение фаз гармоник с сохранением спектров мощности. Формируя разные случайные распределения фаз гармоник в Фурье-разложении сигналов и производя обратное Фурье-преобразование, генерируют N пар (типично, 100 или 1000 пар) суррогатных сигналов, длина которых равна длине экспериментальных данных, спектральные свойства эквивалентны им, но связи между сигналами в суррогатных данных заведомо разрушены. По сформированному ансамблю рассчитывают значения S для каждой пары суррогатных временных рядов. Таким образом, ненулевые значения S для суррогатных данных могут быть получены только благодаря случайному совпадению мгновенных частот колебаний. Если рассчитанное по экспериментальным данным значение S превышает значения, рассчитанные по суррогатным данным, то статистическая гипотеза о несвязанных сигналах считается опровергнутой. Т.е. можно утверждать, что рассчитанное значение S не случайно и определяется именно взаимодействием систем, породивших анализируемые сигналы.

Формально говорят, что рассчитанное значение S опровергает статистическую гипотезу о несвязанных системах, например, c вероятностью 0,95, если рассчитанное по экспериментальным данным значение S превышает не менее 95% значений индексов, рассчитанных по суррогатным данным. В этом случае используют также формулировку: величина индекса статистически значима на уровне p>0,05. Например, если размер ансамбля суррогатных данных N=100, то для того, чтобы рассчитанное по данным значение S было статистически значимо на уровне p>0,05 необходимо, чтобы его величина превышала 95 значений индексов рассчитанных по такому ансамблю суррогатных данных. Выбор уровня значимости p>0,05 означает, что не более 5% значений индексов, рассчитываемых по экспериментальным данным, определяются случайными флуктуациями, а не наличием фазовой синхронизации [92]. Выбор уровня значимости определяется особенностями постановки исследовательской задачи, типичен выбор уровней значимости 0,05 или 0,01 (когда допускается не более 1% случайных выводов).

Получение незначимого результата говорит не об отсутствии синхронизации, а о том, что данный метод анализа не позволяет получить достоверный вывод о ее наличии по конкретной паре временных рядов (это может быть связано с высоким уровнем шумов и искажений в сигналах, недостаточной длительностью записи и другими факторами).

Для контроля статистической значимости результатов могут использоваться и другие методы приготовления суррогатных данных. Например, широко используются подход, основанный на случайном перемешивании мгновенных фаз сигналов интервалами по 2π [93], или метод, основанный на случайной выборке экспериментальных реализаций из ансамбля записей однородной группы испытуемых (т.е. один сигнал от одного человека, другой, от другого) [94]. Используются и другие методы, проверяющие разные статистические гипотезы и основанные на различных априорных предположениях о свойствах данных [87-89].

 

Результаты

С помощью предложенного метода (см. раздел «Анализ фазовой синхронизации 0,1 Гц-колебаний в ВРС и ФПГ») был рассчитан суммарный процент S фазовой синхронизации 0,1 Гц-колебаний в ВРС и ФПГ для всех обследуемых. Пример обработки и анализа данных здорового субъекта представлен на рисунке 8.

 

   
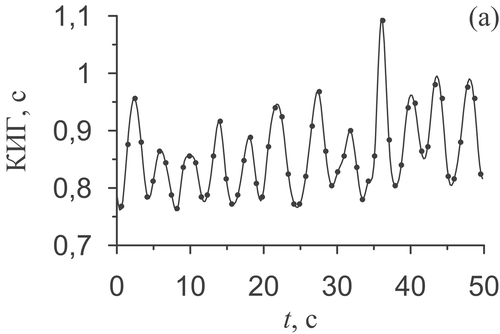
Рисунок 8 (часть 1). Результаты работы предложенного метода диагностики фазовой синхронизации для мужчины 25 лет без патологий ССС. (а) – КИГ, т.е. последовательность длительностей RR-интервалов (точки), и ее аппроксимация с помощью кубических сплайнов для получения эквидистантной КИГ. (б) – ФПГ. (в) и (г) – спектры мощности эквидистантной КИГ и ФПГ, соответственно. Вертикальная пунктирная линия отмечает 0,1 Гц – центр полосы фильтрации сигналов.

 

   
Рисунок 8 (часть 2). Результаты работы предложенного метода диагностики фазовой синхронизации для мужчины 25 лет без патологий ССС. (д) и (е) – сигналы x(t) и y(t) – результат фильтрации в полосе 0,05-0,15 Гц сигналов КИГ и ФПГ (сплошная линия), преобразования Гильберта сигналов представлены пунктиром. (ж) – мгновенные фазы сигналов: x(t) – сплошная линия, y(t) – пунктирная линия. (з) – разность мгновенных фаз сигналов x(t) и y(t). Скобки отмечают найденные интервалы фазовой синхронизации.

 

На рисунке 9а представлены распределения значений показателя S в исследуемых группах здоровых лиц и пациентов, перенесших инфаркт миокарда три недели назад. При этом у здоровых людей показатель S имеет в среднем более высокие значения (33,3±16,2%, представлено как М±σ), чем у пациентов (15,7±9,4%), что согласуется с ранее полученными нами данными [18]. Таким образом, предложенный метод (см. раздел «Анализ фазовой синхронизации 0,1 Гц-колебаний в ВРС и ФПГ») обеспечивает удовлетворительное качество разделения групп лиц с различным функциональным состоянием ССС (в частности, здоровых лиц и пациентов, перенесших инфаркт миокарда).

 


Рисунок 9. Гистограммы распределения суммарного процента фазовой синхронизации S между 0,1 Гц-колебаниями в ВРС и ФПГ у здоровых людей (сплошная линия) и пациентов, перенесших инфаркт миокарда (3-я неделя течения заболевания), (пунктирная линия). (а) – оценка по всей выборке; (б) – выборке значимых результатов (р<0,05).

 

При этом только около половины значений показателя синхронизации S и у здоровых лиц, и у пациентов, перенесших инфаркт миокарда, оказались статистически значимыми (p<0,05) при проверке на основе суррогатных данных. Оказалось, что контроль статистической значимости результатов исследования синхронизации позволяет повысить чувствительность методики. Сопоставление рисунка 9а и рисунка 9б показывает, что отбор значимых результатов позволяет улучшить кластеризацию испытуемых по их статусу здоровья (здоровые лица, и пациенты, перенесшие инфаркт миокарда): значение S в группе здоровых лиц составило 45,7±12,5% (М±σ), а в группе пациентов с перенесенным инфарктом миокарда – 19,9±12,0%. Таким образом, контроль статистической значимости количественной меры синхронизации 0,1 Гц-колебаний в ВРС и ФПГ повышает эффективность предложенной методики.

Однако в ряде случаев определением статистической значимости показателя S на основе суррогатных данных можно пренебречь, учитывая, что ее низкий уровень не является доказательством некорректности полученного значения показателя, свидетельствуя только об отсутствии статистических доказательств его корректности. В качестве альтернативы можно использовать эмпирически подобранное пороговое значение показателя – Sc.

Выбор данного значения основан на предположении, что когда индекс синхронизации 0,1 Гц-колебаний в ВРС и ФПГ менее Sc, механизмы вегетативной регуляции не могут обеспечить функциональную целостность ССС, снижая в целом ее адаптационные возможности. Поэтому значения показателя S менее Sc позволяют судить о значимой десинхронизации 0,1 Гц-колебаний, независимо от результатов оценки статистической значимости.

Анализ всех 1056 записей показал, что данный «критический» уровень показателя синхронизации S может находиться на уровне около 25% (рисунок 10). При этом значения S≤25% могут свидетельствовать о значительной десинхронизации 0,1 Гц-колебаний. Дополнительным основанием правомерности такого подхода являются результаты оценки условной вероятности получения статистически значимых результатов в зависимости от значений показателя S в изучаемых записях (рисунок 11). В исследуемом массиве записей доля статистически значимых результатов метода в диапазоне значений S≤25% составила 21,9%, а в диапазоне S>25% – 67,4%. Таким образом, при значениях показателя синхронизации S>25%, независимо от состояния здоровья пациента, для ~68% случаев (т.е. на уровне ±σ) – уровень статистической значимости р будет <0,05, что можно принять достаточным для интерпретации результатов исследований. Данный подход может быть оправдан при проведении исследований, когда по различным причинам оценка показателя S производится ретроспективно и нет возможности повторной регистрации необходимых биологических сигналов у каждого конкретного пациента.

 


Рисунок 10. Зависимость уровня статистической значимости от значений суммарного процента синхронизации S. Серым цветом выделена область значений S≤25%. Горизонтальной линией ограничен уровень значимости р=0,05.

 

Отметим, что в соответствии с рисунком 11 пороговый уровень суммарного процента синхронизации (Sc) можно выбрать и отличный от 25%, применительно к конкретным задачам исследования. В частности, при анализе прогностической значимости индекса S у пациентов, перенесших инфаркт миокарда, уровень Sc был установлен на отметке 20%, что позволяло повысить эффективность оценки риска [34, 35].

 


Рисунок 11. Условная вероятность получения статистически значимого вывода о наличии синхронизации для выбранного значения показателя S.

 

Однако предложенный альтернативный подход к оценке результатов исследования синхронизации 0,1 Гц-колебаний в ВРС и ФПГ имеет важное ограничение к применению – невозможность оценки достоверности получаемых результатов для каждого пациента в отдельности. Поэтому при изучении синхронизации 0,1 Гц-колебаний у пациента индивидуально следует производить перерегистрацию сигналов ЭКГ и ФПГ для получения статистически значимого результата.

Предложенный метод, по нашему мнению, имеет потенциальную перспективность для клинической кардиологии и нуждается в детальном изучении его диагностических возможностей в последующих исследованиях.

 

Заключение

В представленной работе подробно описан метод количественной оценки степени синхронизации 0,1 Гц-колебаний в ВРС и ФПГ, основанный на автоматизированном поиске пологих участков разностей мгновенных фаз колебаний с последующим вычислением суммарного процента фазовой синхронизации – индекса S. Показано, что контроль статистической значимости (на основе суррогатных данных) результатов предложенного метода повышает чувствительность методики, что особенно важно в индивидуальной клинической практике.

На описанную методику получен Патент на изобретение № 2374986 (РФ) от 10.12.2008 г. (приоритет от 22.07.2008).

 

Конфликт интересов: не заявляется.

 

Благодарности

Статья написана при поддержке гранта Президента РФ МД-4368.2015.7, а также РФФИ № 15-02-03061 и № 16-32-00326.

Библиографический список: 
  1. Special focus issue on cardiovascular physics edited by N. Wessel, J. Kurths, W. Ditto, and R. Bauernschmitt. Chaos 2007; 17(1).
  2. Heart rate variability: standards of measurement, physiological interpretation and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Circulation 1996; 93: 1043–1065. (PMID: 8598068) (doi: 10.1161/01.CIR.93.5.1043)
  3. Parati G., Saul J.P., Di Rienzo M., Mancia G. Spectral analysis of blood pressure and heart rate variability in evaluating cardiovascular regulation. A critical appraisal. Hypertension 1995; 25: 1276–1286. (PMID: 7768574) (doi: 10.1161/01.HYP.25.6.1276)
  4. Hilsted J. Peripheral blood flow control in diabetes mellitus. Acta Physiol Scand Suppl 1991; 603: 47-51. (PMID: 1789129)
  5. Nishihara N., Iwakiri H., Ogiuchi H., Ozaki M. Diagnosis of the autonomic nervous function during sedation by peripheral blood flow and psychogenic perspiration. Masui 2003; 52: 128-134. Japanese (PMID: 12649866)
  6. Коряков В.В. Инструментальная диагностика и комплексное лечение гипервентиляционного синдрома. Терапевтический архив 2012; 84(3): 28-31. (PMID: 22708419)
  7. Zhang Q., Patwardhan A.R., Knapp C.F., Evans J.M. Cardiovascular and cardiorespiratory phase synchronization in normovolemic and hypovolemic humans. Eur J Appl Physiol 2015; 115: 417-427. (PMID: 25344797) (doi: 10.1007/s00421-014-3017-4)
  8. Prokhorov M.D., Ponomarenko V.I., Gridnev V.I., et al. Synchronization between main rhythmic processes in the human cardiovascular system. Phys Rev E 2003; 68: 041913. (PMID: 14682979)
  9. Karavaev A.S., Prokhorov M.D., Ponomarenko V.I., et al. Synchronization of low-frequency oscillations in the human cardiovascular system. Chaos 2009; 19: 033112. (doi: 10.1063/1.3187794) (PMID: 19791992) [PDF]
  10. Кирилина Т.В., Красников Г.В., Танканаг А.В. и др. Пространственная синхронизация колебаний кровотока в системе микроциркуляции кожи человека. Регионарное кровообращение и микроциркуляция 2009; 8(3): 32-36.
  11. Киселев А.Р., Гриднев В.И. Колебательные процессы в вегетативной регуляции сердечно-сосудистой системы. Саратовский научно-медицинский журнал 2011; 7(1): 34-39. [PDF]
  12. Orini M., Bailón R., Mainardi L.T., Laguna P. Time-frequency phase differences and phase locking to char-acterize dynamic interactions between cardiovascular signals. Conf Proc IEEE Eng Med Biol Soc 2011; 2011: 4689-4692. (doi: 10.1109/IEMBS.2011.6091161) (PMID: 22255384)
  13. Liao F., Jan Y.K. Enhanced phase synchronization of blood flow oscillations between heated and adjacent non-heated sacral skin. Med Biol Eng Comput 2012; 50: 1059–1070. (PMID: 22936012) (PMCID: PMC3469726) (doi: 10.1007/s11517-012-0948-y)
  14. Seidel H., Herzel H. Bifurcations in a nonlinear model of the baroreceptor-cardiac reflex. Physica D: Nonlinear Phenomena 1998; 115: 145-160. (doi: 10.1016/S0167-2789(97)00229-7)
  15. Ottesen J.T. Modelling the dynamical baroreflex-feedback control. Mathematical and Computer Modelling 2000; 31: 167-173. (doi: 10.1016/S0895-7177(00)00035-2)
  16. Kotani K., Struzik Z.R., Takamasu K., et al. Model for complex heart rate dynamics in health and disease. Physical Review E 2005; 72: 041904. (doi: 10.1103/PhysRevE.72.041904)
  17. Silvani A., Magosso E., Bastianini S., et al. Mathematical modeling of cardiovascular coupling: Central autonomic commands and baroreflex control. Auton Neurosci 2011; 162: 66-71. (PMID: 21550860) (doi: 10.1016/j.autneu.2011.04.003)
  18. Киселев А.Р., Беспятов А.Б., Посненкова О.М. и др. Внутренняя синхронизация основных 0,1 Гц-частотных ритмов в системе вегетативного управления сердечно-сосудистой системой. Физиология человека 2007; 33(2): 69-75. (PMID: 17486991) [PDF]
  19. deBoer R.W., Karemaker J.M., Strackee J. Hemodynamic fluctuations and baroreflex sensitivity in humans: a beat-to-beat model. Am J Physiol 1987; 253: H680- H689. (PMID: 3631301)
  20. Montano N., Gnecchi-Ruscone T., Porta A., et al. Presence of vasomotor and respiratory rhythms in the discharge of single medullary neurons involved in the regulation of cardiovascular system. J Auton Nerv Syst 1996; 57: 116-122. (PMID: 8867094)
  21. Cooley R.L., Montano N., Cogliati C., et al. Evidence for a central origin of the low-frequency oscillation in RR-interval variability. Circulation 1998; 98: 556-561. (PMID: 9714113) (doi: 10.1161/01.CIR.98.6.556)
  22. Whittam A.M., Claytont R.H., Lord S.W., et al. Heart rate and blood pressure variability in normal subjects com-pared with data from beat-to-beat models developed from de Boer’s model of the cardiovascular system. Physiol Meas 2000; 21: 305-318. (PMID: 10847197) (doi: 10.1088/0967-3334/21/2/310)
  23. Cohen M.A., Taylor J.A. Short-term cardiovascular oscillations in man: Measuring and modeling the physiologies. J Physiol (London) 2002; 542: 669-683. (PMID: 12154170) (doi:  10.1113/jphysiol.2002.017483) (PMCID: PMC2290446)
  24. Malpas S. Neural influences on cardiovascular variability: Possibilities and pitfalls. Am J Physiol Heart Circ Physiol 2002; 282: H6-H20. (PMID: 11748042)
  25. Гриднев В.И., Киселев А.Р., Котельникова Е.В. и др. Влияние внешних периодических стимулов на вариабельность сердечного ритма у здоровых лиц и у пациентов с ишемической болезнью сердца. Физиология человека 2006; 32(5): 74-83. (PMID: 17100343) [PDF]
  26. Bernardi L., Radaelli A., Solda P.L., et al. Autonomic control of skin microvessels: assessment by power spectrum of photoplethysmographic waves. Clin Sci (London) 1996; 90: 345–355. (PMID: 8665771) (doi: 10.1042/cs0900345)
  27. Middleton P.M., Chan G.S., Steel E., et al. Fingertip photoplethysmographic waveform variability and systemic vascular resistance in intensive care unit patients. Med Biol Eng Comput 2011; 49: 859–866. (doi: 10.1007/s11517-011-0749-8) (PMID: 21340639)
  28. Middleton P.M., Tang C.H., Chan G.S., et al. Peripheral photoplethysmogra-phy variability analysis of sepsis patients. Med Biol Eng Comput 2011; 49: 337–347. (doi: 10.1007/s11517-010-0713-z) (PMID: 21153887)
  29. Rhee S., Yang B.H., Asada H. Theoretical evaluation of the influence of displacement on finger photoplethysmography for wearable health monitoring sensors. In: Symposium on Dynamics, Control, and Design of Biomechanical Systems ASME International Mechanical Engineering Congress and Exposition, Nashville, Tennessee, November 14-19, 1999.
  30. Bernardi L., Hayoz D., Wenzel R., et al. Synchronous and baroceptor-sensitive oscillations in skin microcirculation: evidence for central autonomic control. Am J Physiol Heart Circ Physiol 1997; 273: 1867-1878. (PMID: 9362255)
  31. González H., Infante O., Lerma C. Response to active standing of heart beat interval, systolic blood volume and systolic blood pressure: recurrence plot analysis Translational Recurrences. Springer Proceedings in Mathematics & Statistics 2014; 103: 109-123. (doi: 10.1007/978-3-319-09531-8_7)
  32. Millasseau S.C., Guigui F.G., Kelly R.P., et al. Noninvasive assessment of the digital volume pulse. Comparison with the peripheral pressure pulse. Hypertension 2000; 36: 952–956. (PMID: 11116106) (doi: 10.1161/01.HYP.36.6.952)
  33. Караваев А.С., Киселев А.Р., Гриднев В.И. и др. Фазовый и частотный захват 0,1 Гц-колебаний в ритме сердца и барорефлекторной регуляции артериального давления дыханием с линейно меняющейся частотой у здоровых лиц. Физиология человека 2013; 39(4): 93–104. (PMID: 25486835) [PDF]
  34. Kiselev A.R., Gridnev V.I., Prokhorov M.D., et al. Evaluation of 5-year risk of cardiovascular events in patients after acute myocardial infarction using synchronization of 0.1-Hz rhythms in cardiovascular system. Ann Noninvasive Electrocardiol 2012; 17(3): 204–213. (PMID: 22816539) (doi: 10.1111/j.1542-474X.2012.00514.x) [PDF]
  35. Киселев А.Р., Гриднев В.И., Караваев А.С. и др. Оценка пятилетнего риска летального исхода и развития сердечно-сосудистых событий у пациентов с острым инфарктом миокарда на основе синхронизации 0,1 Гц-ритмов в сердечно-сосудистой системе. Саратовский научно-медицинский журнал 2010; 6: 328-338. [PDF]
  36. Киселев А.Р., Гриднев В.И., Посненкова О.М. и др. Оценка на основе определения синхронизации низкочастотных ритмов динамики вегетативной регуляции сердечно-сосудистой системы при применении метопролола у больных ИБС, перенесших инфаркт миокарда. Терапевтический архив 2007; 79(4): 23-31. (PMID: 17564014) [PDF]
  37. Киселев А.Р., Гриднев В.И., Караваев А.С. и др. Влияние карведилола и метопролола на функциональное взаимодействие механизмов вегетативной регуляции сердца и микроциркуляции крови у больных артериальной гипертонией и избыточной массой тела. Рациональная фармакотерапия в кардиологии 2009; (3): 55-61. [PDF]
  38. Kiselev A.R., Gridnev V.I., Prokhorov M.D., et al. Selection of optimal dose of beta-blocker treatment in myocardial infarction patients based on changes in synchronization between 0.1 Hz oscillations in heart rate and peripheral microcirculation. J Cardiovasc Med 2012; 13: 491-498. (doi: 10.2459/JCM.0b013e3283512199) (PMID: 22343262) [PDF]
  39. Kiselev A.R., Gridnev V.I., Prokhorov M.D., et al. Effects of antihypertensive treatment on cardiovascular autonomic control. Anadolu Kardiyol Derg 2014; 14: 701-710. (PMID: 25188759) (doi: 10.5152/akd.2014.5107) [PDF]
  40. Нейфельд И.В., Киселев А.Р., Караваев А.С. и др. Особенности показателей вегетативной регуляции кровообращения и вариабельности сердечного ритма у женщин в перименопаузе. Анналы аритмологии 2014; 11(2): 98-108. (doi: 10.15275/annaritmol.2014.2.4) [PDF]
  41. Neufeld I.W., Kiselev A.R., Karavaev A.S., et al. Autonomic control of cardiovascular system in pre- and postmenopausal women: a cross-sectional study. J Turk Ger Gynecol Assoc 2015; 16: 11-20. (doi: 10.5152/jtgga.2015.15201) (PMID: 25788843) [PDF]
  42. Шварц В.А., Киселев А.Р., Караваев А.С. и др. Изучение динамики нелинейных свойств системы барорефлекторной регуляции кровообращения у больных, перенесших операцию аорто-коронарного шунтирования (дизайн исследования). Бюллетень медицинских интернет‐конференций 2014; 4(9): 1042-1048. [PDF]
  43. Баевский Р.М., Иванов Г.Г., Чирейкин Л.В. и др. Анализ вариабельности сердечного ритма при использовании различных электрокардиографических систем (часть 1). Вестник аритмологии 2002; (24): 65-86.
  44. Безручко Б.П., Смирнов Д.А. Математическое моделирование и хаотические временные ряды. Саратов: ГосУНЦ "Колледж", 2005; 299 с.
  45. Bezruchko B.P., Smirnov D.A. Extracting knowledge from time series (an introduction to nonlinear empirical modeling). Berlin, Germany: Springer-Verlag Berlin Heidelberg, 2010; 405 p. (doi: 10.1007/978-3-642-12601-7)
  46. Малинецкий Г., Потапов А., Подлазов А. Нелинейная динамика: подходы, результаты, надежды. M.: Либроком, 2011; 280 c.
  47. Трубецков Д.И. Введение в синергетику. Колебания и волны. M.: Либроком, 2011; 224 с.
  48. Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны (учебное пособие). М.: Физматлит, 2001; 416 с.
  49. Пиковский А., Розенблюм М., Куртс Ю. Синхронизация: фундаментальное нелинейное явление. М.: Техносфера, 2003; 496 c.
  50. Umapathy K., Nair K., Masse S., et al. Phase mapping of cardiac fibrillation. Circ Arrhythm Electrophysiol 2010; 3: 105-114. (PMID: 20160178) (doi: 10.1161/CIRCEP.110.853804)
  51. Latka M., Turalska M., Glaubic-Latka M., et al. Phase dynamics in cerebral autoregulation. Am J Physiol Heart Circ Physiol 2005; 289: H2272- H2279. (PMID: 16024579) (doi: 10.1152/ajpheart.01307.2004)
  52. Kantz H., Kurths J., Mayer-Kress G. Nonlinear analysis of physiological data. Berlin, Germany: Springer Berlin Heidelberg, 2012; 344 p. (doi: 10.1007/978-3-642-71949-3)
  53. Laughner J.I., Ng F.S., Sulkin M.S., et al. Processing and analysis of cardiac optical mapping data obtained with potentiometric dyes. Am J Physiol Heart Circ Physiol 2012; 303: H753–H765. (PMID: 22821993) (doi: 10.1152/ajpheart.00404.2012)
  54. Cohen L. Time-frequency analysis electrical engineering signal processing. Prentice Hall PTR, 1995; 299 p.
  55. Zhang Y., Wang S., Ji G., Dong Z. An improved quality guided phase unwrapping method and its applications to MRI. Progress In Electromagnetics Research 2014; 145: 273-286. (doi: 10.2528/PIER14021005)
  56. Taner M.T., Koehler F., Sheriff R.E. Complex seismic trace analysis. Geophysics 1979; 44: 1041-1063. (doi: 10.1190/1.1440994)
  57. Ifeachor E.C., Jervis B.W. Digital signal processing: a practical approach (2nd Edition). Prentice Hall, 2002; 933 p.
  58. Gabor D. Theory of communication. Part 1: The analysis of information. Journal of the Institution of Electrical Engineers - Part III: Radio and Communication Engineering 1946; 93(26): 429-441. (doi: 10.1049/ji-3-2.1946.0074)
  59. Хованов И.А., Хованова Н.А. Методы обработки временных рядов (учебное пособие). Саратов: Изд. ГосУНЦ "Колледж", 2001; 120 с.
  60. Tass P., Smirnov D., Karavaev A., et al. The causal relationship between subcortical local field potential oscillations and Parkinsonian resting tremor. J Neural Eng 2010; 7(1): 16009. (PMID: 20083863) (doi: 10.1088/1741-2560/7/1/016009)
  61. Киселев А.Р., Хорев В.С., Гриднев В.И. и др. Взаимодействие 0,1 Гц-колебаний в вариабельности ритма сердца и вариабельности кровенаполнения дистального сосудистого русла. Физиология человека 2012; 38(3): 92-99. (PMID: 22830248) [PDF]
  62. Mase M., Glass L., Disertori M., Ravelli F. The AV synchrogram: a novel approach to quantify atrioventricular coupling during atrial arrhythmias. Biomedical Signal Processing and Control 2013; 8(6): 1008–1016. (doi: 10.1016/j.bspc.2013.01.004)
  63. Tallon-Baudry C., Bertrand O., Fischer C. Oscillatory synchrony between human extrastriate areas during visual short-term memory maintenance. J Neurosci 2001; 21(20): RC177. (PMID: 11588207)
  64. Rosenblum M.G., Pikovsky A.S., Kurths J., et al. Phase synchronization: from theory to data analysis. In: Neuro-informatics, edited by F. Moss and S. Gielen. Handbook of Biological Physics. Vol. 4. New York: Elsevier Science, 2000: 279-321.
  65. Quian Quiroga R., Kreuz T., Grassberger P. Event synchronization: a simple and fast method to measure synchronicity and time delay patterns. Phys Rev E 2002; 66: 041904. (doi: 10.1103/PhysRevE.66.041904)
  66. Pikovskii A.S. Synchronization and stochastization of array of self-excited oscillators by external noise. Radiophys Quantum Electron 1984; 27(5): 390-395. (doi: 10.1007/BF01044784)
  67. Pikovskii A. On the interaction of strange attractors.  Zeitschrift für Physik B Condensed Matter 1984; 55(2): 149-154. (doi: 10.1007/BF01420567)
  68. Afraimovich V.S., Verichev N.N., Rabinovich M.I. Stochastic synchronization of oscillations in dissipative systems. Radiophys Quantum Electron 1986; 29(9): 795-803. (doi: 10.1007/BF01034476)
  69. Aranson I.S., Rul'kov N.F. Nontrivial structure of synchronization zones in multidimensional systems. Phys Lett A 1989; 139(8): 375-378. (doi: 10.1016/0375-9601(89)90581-1)
  70. Pecora L.M., Carroll T.L. Synchronization of chaotic systems. Chaos 2015; 25: 097611. (doi: 10.1063/1.4917383)
  71. Rosenblum M.G., Kurths J., Pikovsky A., et al. Synchronization in noisy systems and cardiorespiratory interaction. Engineering in Medicine and Biology 1998; 17(6): 46-53. (doi: 10.1109/51.731320)
  72. Tass P., Rosenblum M.G., Weule J., et al. Detection of n:m phase locking from noisy data: application to magnetoencephalography. Phys Rev Lett 1998; 81: 3291-3294. (doi: 10.1103/PhysRevLett.81.3291)
  73. Wu M.C., Hu C.K. Empirical mode decomposition and synchrogram approach to cardiorespiratory synchronization. Physical Review E 2006; 73: 051917. (doi: 10.1103/PhysRevE.73.051917)
  74. White L.B., Boashash B. Cross spectral analysis of nonstationary processes. IEEE Transactions on Information Theory 1990; 36: 830-835. (doi: 10.1109/18.53742)
  75. Schafer C., Rosenblum M.G., Abel H.H., Kurths J. Synchronization in the human cardiorespiratory system. Physical Review E 1999; 60: 857–870. (PMID: 11969830) (doi: 10.1103/PhysRevE.60.857)
  76. Bartsch R., Kantelhardt J.W., Penzel T., Havlin S. Experimental evidence for phase synchronization transitions in the human cardiorespiratory system. Phys Rev Lett 2007; 98: 054102. (PMID: 17358862) (doi: 10.1103/PhysRevLett.98.054102)
  77. Hramov A.E., Koronovskii A.A., Ponomarenko V.I., Prokhorov M.D. Detection of synchronization from univariate data using wavelet transform. Phys Rev E 2007; 75: 056207. (doi: 10.1103/PhysRevE.75.056207)
  78. Hramov A.E., Koronovsky A.A., Ponomarenko V.I., Prokhorov M.D. Detecting synchronization of self-sustained oscillators by external driving with varying frequency. Phys Rev E 2006; 73: 026208. (doi: 10.1103/PhysRevE.73.026208)
  79. Короновский А.А., Пономаренко В.И., Прохоров М.Д., Храмов А.Е. Диагностика синхронизации автоколебательных систем при изменении частоты внешнего воздействия с использованием вейвлетного анализа. Радиотехника и электроника 2007; 52(5): 581-592. 
  80. Короновский А.А., Пономаренко В.И., Прохоров М.Д., Храмов А.Е. Метод исследования синхронизации автоколебаний по унивариантным данным с использованием непрерывного вейвлетного анализа. Журнал технической физики 2007; 77(9): 6-15.
  81. Безручко Б.П., Гриднев В.И., Караваев А.С. и др. Методика исследования синхронизации колебательных процессов с частотой 0,1 Гц в сердечно-сосудистой системе человека. Известия высших учебных заведений. Прикладная нелинейная динамика 2009; 17(6): 44-56.
  82. Боровкова Е.И., Караваев А.С., Пономаренко В.И., Прохоров М.Д. Сопоставление методов диагностики фазовой синхронизованности по тестовым данным, моделирующим нестационарные сигналы биологической природы. Известия Саратовского Университета. Новая серия. Серия Физика 2015; 15(3): 36-42. (doi: 10.18500/1817-3020-2015-15-3-36-42)
  83. Кульминский Д.Д., Боровкова Е.И., Хорев В.С., Миронов С.А. Разработка устройства суточного мониторинга состояния сердечно-сосудистой системы на основе анализа синхронизации ее ритмов. Бюллетень медицинских интернет-конференций 2014; 4(7): 962-966.
  84. Кульминский Д.Д., Астахов О.В., Боровкова Е.И., Киселев А.Р.  Диагностика состояния сердечнососудистой системы на основе оценки степени синхронизованности ее ритмов по унивариантному сигналу фотоплетизмограммы. В кн.: Сборник материалов Всероссийской молодежной научной конференции «Актуальные вопросы биомедицинской инженерии». Саратов, 2013: 330-335.
  85. Боровкова Е.И., Караваев А.С., Киселев А.Р. и др. Метод диагностики синхронизованности 0,1 Гц ритмов вегетативной регуляции сердечно-сосудистой системы в реальном времени. Анналы аритмологии 2014; 11(2): 129-136. (doi: 10.15275/annaritmol.2014.2.7) [PDF]
  86. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. М.: Физматлит, 1958; 336 с.
  87. Трухачева Н.В. Математическая статистика в медико-биологических исследованиях с применением пакета Statistica. M.: ГЭОТАР-Медиа, 2012; 379 с.
  88. Nait-Ali A. Advanced Biosignal Processing. Springer Science & Business Media, 2009; 378 p. (doi: 10.1007/978-3-540-89506-0)
  89. Chan K.-S., Tong H. Chaos: A Statistical Perspective. Springer Series in Statistics. Springer Science & Business Media, 2013; 300 p. (doi: 10.1007/978-1-4757-3464-5)
  90. Theiler J., Eubank S., Longtin A., et al. Testing for nonlinearity in time series: the method of surrogate data. Physica D 1992; 58: 77-94. (doi: 10.1016/0167-2789(92)90102-S)
  91. Schreiber T., Schmitz A. Improved surrogate data for nonlinearity tests. Phys Rev Lett 1996; 77: 635–638. (doi: 10.1103/PhysRevLett.77.635) (PMID: 10062864)
  92. Айвазян С.А. Прикладная статистика. М.: Рипол Классик, 1983; 384 с.
  93. Brea J., Russell D.F., Neiman A.B. Measuring direction in the coupling of biological oscillators: A case study for electroreceptors of paddlefish. Chaos 2006; 16: 026111. (doi: 10.1063/1.2201466) (PMID: 16822043)
  94. Toledo E., Rosenblum M.G., Kurths J., Akselrod S. Cardiorespiratory synchronization: Is it a real phenomenon? In: Computers in Cardiology. A. Murray and S. Swiryn eds. Hannover: IEEE Computer Society Press, 1999: 237-240. (doi: 10.1109/CIC.1999.825950)
Об авторах: 

Киселев Антон Робертович – доктор медицинских наук, ведущий научный сотрудник, Отдел продвижения новых кардиологических информационных технологий, НИИ кардиологии, ГБОУ ВПО Саратовский ГМУ им. В.И. Разумовского Минздрава России, Саратов, Россия; профессор кафедры динамического моделирования и биомедицинской инженерии, ФГБОУ ВО «Саратовский государственный университет им. Н.Г. Чернышевского», Саратов, Россия; научный сотрудник, отделение хирургического лечения интерактивной патологии, ФГБУ «НЦССХ им. А.Н. Бакулева», Москва, Россия.
Караваев Анатолий Сергеевич – кандидат физико-математических наук, доцент, кафедра динамического моделирования и биомедицинской инженерии, ФГБОУ ВО «Саратовский государственный университет им. Н.Г. Чернышевского», Саратов, Россия.
Гриднев Владимир Иванович – доктор медицинских наук, руководитель Отдела продвижения новых кардиологических информационных технологий, НИИ кардиологии, ГБОУ ВПО Саратовский ГМУ им. В.И. Разумовского Минздрава России, Саратов, Россия; профессор кафедры динамического моделирования и биомедицинской инженерии, ФГБОУ ВО «Саратовский государственный университет им. Н.Г. Чернышевского», Саратов, Россия.
Прохоров Михаил Дмитриевич – доктор физико-математических наук, заведующий лабораторией моделирования в нелинейной динамике, Саратовский филиал ФГБУН «Институт радиотехники и электроники им. В.А. Котельникова» РАН, Саратов, Россия.
Пономаренко Владимир Иванович – доктор физико-математических наук, профессор кафедры динамического моделирования и биомедицинской инженерии, ФГБОУ ВО «Саратовский государственный университет им. Н.Г. Чернышевского», Саратов, Россия; ведущий научный сотрудник, лаборатория моделирования в нелинейной динамике, Саратовский филиал ФГБУН «Институт радиотехники и электроники им. В.А. Котельникова» РАН, Саратов, Россия.
Боровкова Екатерина Игоревна – аспирант кафедры динамического моделирования и биомедицинской инженерии, ФГБОУ ВО «Саратовский государственный университет им. Н.Г. Чернышевского», Саратов, Россия.
Шварц Владимир Александрович – кандидат медицинских наук, младший научный сотрудник, отделение хирургического лечения интерактивной патологии, ФГБУ «НЦССХ им. А.Н. Бакулева», Москва, Россия.
Посненкова Ольга Михайловна – кандидат медицинских наук, старший научный сотрудник, Отдел продвижения новых кардиологических информационных технологий, НИИ кардиологии, ГБОУ ВПО Саратовский ГМУ им. В.И. Разумовского Минздрава России, Саратов, Россия.
Безручко Борис Петрович – доктор физико-математических наук, профессор, кафедра динамического моделирования и биомедицинской инженерии, ФГБОУ ВО «Саратовский государственный университет им. Н.Г. Чернышевского», Саратов, Россия.

Поступила в редакцию 12 января 2016. Принята в печать 12 февраля 2016.

© 2016, Киселев А.Р., Караваев А.С., Гриднев В.И., Прохоров М.Д., Пономаренко В.И., Боровкова Е.И., Шварц В.А., Посненкова О.М., Безручко Б.П.
© 2016, Кардио-ИТ

Ответственный автор: Киселев Антон Робертович. Адрес для переписки: НИИ кардиологии, 141, ул. Чернышевского, г. Саратов, 410028, Россия. Тел.: +7 (8452) 201 899. E-mail: kiselev@cardio-it.ru

Авторы: 
Безручко Борис Петрович - Боровкова Екатерина Игоревна - Гриднев Владимир Иванович - Караваев Анатолий Сергеевич - Киселев Антон Робертович - Пономаренко Владимир Иванович - Посненкова Ольга Михайловна - Прохоров Михаил Дмитриевич - Шварц Владимир Александрович